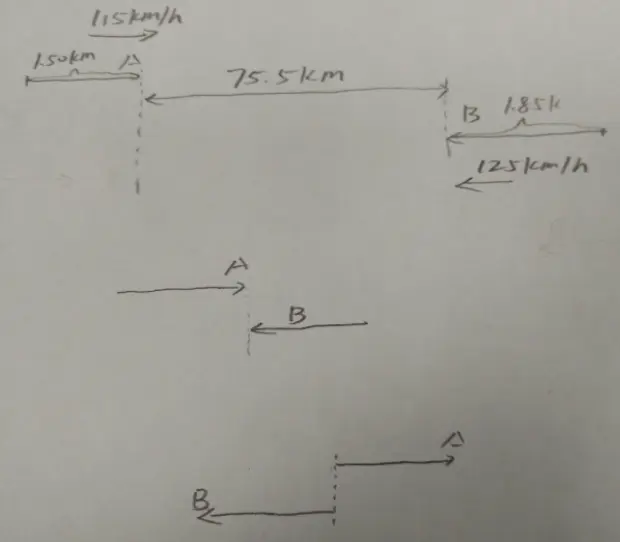
Consider two trains A and B. If train A is 1.50 km long and Train B is 1.85 km long. At the beginning two trains are 75.5 km apart from each other. Then train A and B start move

I've shown two methods for solving this type of questions: graphing and analytical.

Method I: Graphing

(1) Let's study the heads

When two heads meet, $l_A$ is the distance travelled by head A and $l_B$ is the distance travelled by head B.

Let's supoose that it takes t time for two heads to meet.

So we have, $l_A = V_A \times t$
so, $l_A$ = 115 km/h &times t

Also, $l_B = V_B \times t$
so, $l_A$ = 125 km/h &times t

Based on the graph,
$l_A$ + $l_B$ = 75.5

Solving above equations, we get,
t = 0.314 h, $l_A$ = 36.2 km, $l_B$ = 39.3 km

(2) We study the ends of two trains

$l_A^’$ is the distance travelled by end A. $l_B^’$ is the distance travelled by end B. Let's suppose it take t’ for two ends to meet.

$l_A^’$ = 115 km/h × t’
$l_B^’$ = 125 km/h × t’

Based on the graph,
$l_A^’ + l_B^’$ = 1.50 km + 1.85 km + 75.5 km

Solving above equations, we get,
t’ = 0.328 h, $l_A^’$ = 37.8, $l_B^’$ = 41.1 km

---

Method II: Analytical

(1) Let's stydy the heads

First we set up a one dimensional coordinate system axis X. Let the origin O coincide with the end of train A and positive direction is to the right.

So at the beginning, the coordinate of head A is +1.50 km and the coordinate of head B is:
1.50 + 75.5 = 77.0 km

Head A coordinate changes with time t according to following equation,
$X_A$ = 1.50 km + $V_A$t = 1.50 + 115 × t

Head B coordinate changes with time t according to following equation,
$X_B$ = 77.0 km - $V_B$t =77.0 - 125 × t

When they meet, $X_A$ = $X_B$

so, 1.50 + 115 × t = 77.0 - 125 × t
so, t = 0.314 h

And, $l_A$ = $V_A \times t$ = 115 × 0.314 = 36.2 km
also, $l_B$ = $V_B \times t$ = 125 × 0.314 = 39.3 km

(2) We study the ends, and we set up the same coordinate system x axis

So at the beginning, the coordinate for end A is 0 and for end B is
1.50 + 75.5 + 1.85 = 78.85 km

And the coordinate of end A changes along with time,
$X_A^’$ = 115 km/h × t

The coordinate of end B also changes along with time,
$X_B^’$ = 78.85 km - 125 km/h × t

When two end meets, we have,
$X_A^’$ = $X_B^’$
or, 115 × t = 78.85 - 125 × t

so, t = 0.328 h, $l_A^’$ = 37.8 km, $X_B^’$ = 41.4 km

Note: $l_A^’$ and $l_A^’$ can be obtained as we did in method I